Shimmering Wave
Responsibilities: VEX coding, Surface animation, Camera animation, Rendering
Overview
Shimmering Wave is a project that demonstrates how mathematical expressions can be used to create exciting, abstract animated structures without any modeling! While discussing the representation of 3D surfaces in my Calculus 2 class through parametric equations, I became interested in how a surface changes as a parameter grows and how introducing new variables can alter its appearance. My process involved representing the equation of a surface in 3D space using points generated with VEX code, animating their gradual appearance, representing the points as spheres, and creating custom shaders for both the background and spheres using Redshift. The camera animation enhances the experience, making it feel as though the wave is about to catch up with the viewer.

VEX code
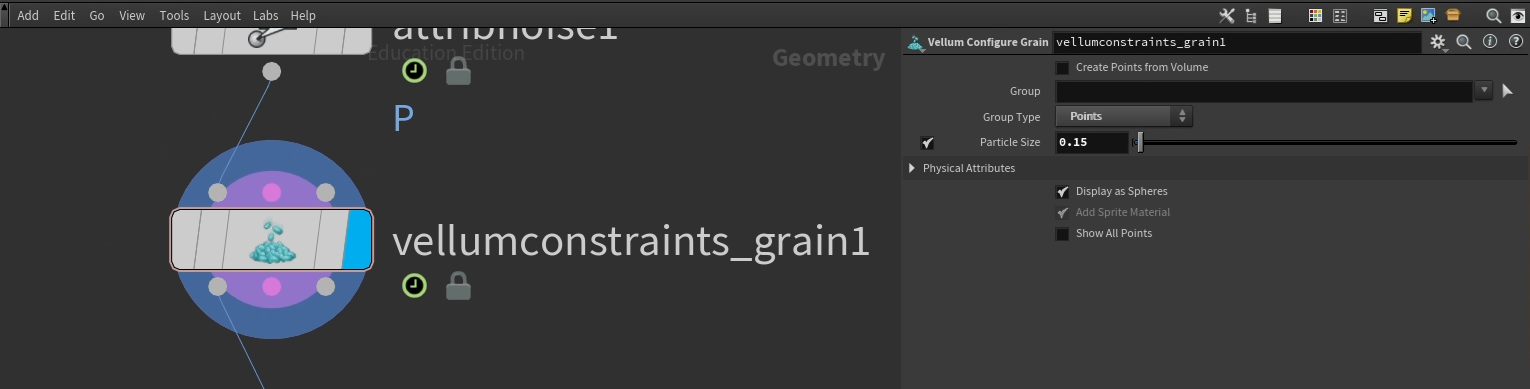
The VEX code creates a dynamic 3D sinusoidal surface by iterating through a grid of points in the x-y plane and calculating their z-coordinates based on a mathematical expression. Using nested for loops, I iterated over a range of values for x and y, scaling them to control the spacing of the grid. For each (x, y) pair, the z value was calculated as z = t * (sin(x) + sin(y)), where t introduces a time-dependent progression, adding variation to the height (z) across iterations.
Each calculated position was then combined into a vector and added to the geometry with the addpoint function, resulting in a dense, wavy surface. The grid's size is dynamically adjustable by modifying the multiples applied to x and y. The wave height can be controlled by adjusting the value of t, while the resolution of the surface can be fine-tuned by altering the loop range and step size. This method offers flexibility and efficiency, making it ideal for procedural modeling.

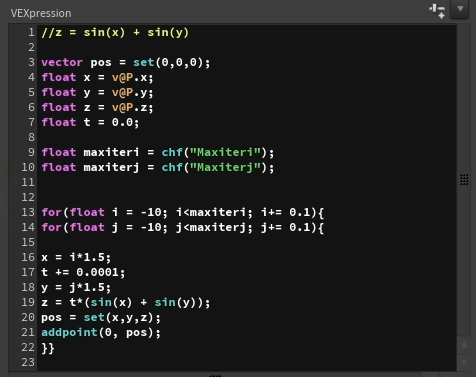
Adding irregularity to the position and scale
Perfection does not exist in the real world and therefore shouldn't in 3D! To introduce a sense of imperfection into my wave, I used the Attribute Noise node with Simplex Noise to subtly shift the positions (P attribute) of the points. This helped create slight variations in the surface, making it feel more organic. I also employed the Attribute Randomize node to randomize the pscale attribute, varying the size of the spheres.
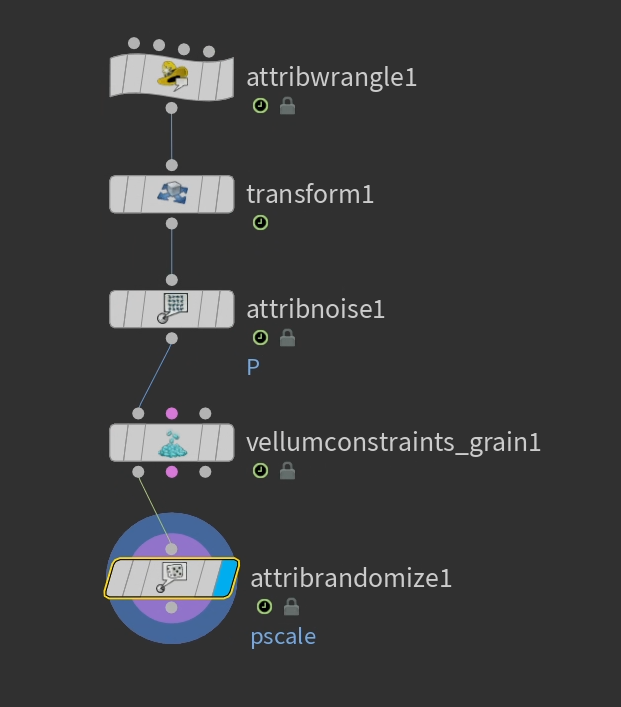

Rendering
I set keyframes and adjusted the values along all axes to make the camera move diagonally, following the flow of the waves across the surface. To really sell the feeling that the wave was about to catch up with the viewer, I animated the focus distance to increase. For lighting, I placed a large area light to brighten the entire scene, with two smaller lights positioned as key and fill to create some depth and highlight the details. I also got creative with materials, using a Ramp node to craft a custom gradient for the background, and designed bubbles to match the style of the scene.

Challenges and learning outcomes
One challenge I faced was finding an efficient way to add geometry to the generated points.
Initially, I used the CopytoPoints node with sphere geometry, but this was very slow and inefficient for simulation. To solve this, I switched to using the Vellum Configure Grains node, which treated the geometry as grains. This method significantly improved performance and allowed for faster, more efficient simulations.